Researchers

Roger Brockett

Abdol-Reza Mansouri

Demos

Demos

Pattern Generation

Introduction

The word "pattern" is used to denote a collection of periodic, or nearly periodic, vector valued functions of time. The choice of the words is inspired by language used in neuroscience and biological motor control where approximate periodicity is common and true periodicity is rare. In fact, for the applications we have in mind, it is only the qualitative properties of the functions that matter; successive cycles need not have exactly the same waveform and/or the same period as long as they possess the appropriate general shape. We argue that the need for, and use of, patterns is closely related to nonlinear effects. We adopt a point of view that unifies and explains these problems in terms of concepts from geometric nonlinear control.

Biped Locomotion

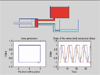
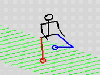
The set of differential equations given below generate biped walking motion. The first four state variables represent the vertical and horizontal components of the right and left feet. x5 represents the velocity of the person's center of mass, while x6 represents the phase between the two feet. e is the target velocity.

Equations for biped locomotion

The interesting property of these equations is that they describe a set of small cyclic motions, in this case the movement of the left and right feet, which give rise to a larger motion of the entire body.

Publications